Задача №6 в учебнике на стр.116
Ахиллес бежит за черепахой со скоростью 3м/с. Между ними 100м.
На какой по счету секунде Ахиллес догонит черепаху, которая ползет в 100 раз медленнее, чем бежит Ахиллес?
Немножко теории:
Формула «скорость, время. расстояние»:
S = V×t.
В данной формуле S — это путь, V — скорость, а t — время.
В данной задаче главная трудность в том, что черепаха тоже ползет, пока Ахиллес бежит.
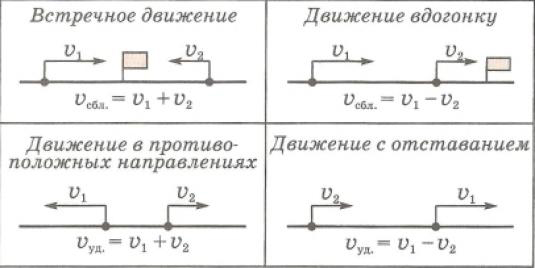
Чтобы «нейтрализовать» черепаху нужно найти скорость сближения.
Скорость сближения — это расстояние, на которое сближаются объекты за единицу времени. Единицей измерения является км/ч, м/с и др. При равномерном движении объектов с разными скоростями расстояние между данными объектами либо увеличивается, либо уменьшается на одно и то же число единиц.
Для решения данной задачи подходит такая формула:
Решаем задачу.
Переведем для удобства скорость движения Ахиллеса в см/с
Тогда: скорость Ахиллеса – 300 см/с, черепахи – 3 см/с.
Узнаем скорость сближения.
300-3 = 297 см/с
Переводим расстояние в см – 100м = 10000см
Находим время за которое Ахиллес догонит черепаху.
10000 : 297 = 33,6700336700…. (с)
Ответ: Ахиллес догонит черепаху на 34-ой секунде.



спасибо