Условие задачи № 564 в учебнике стр. 125
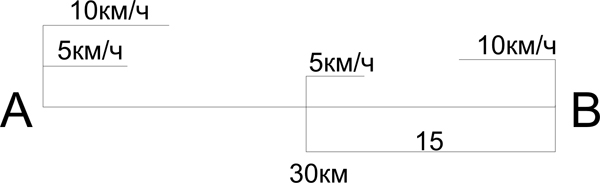
А) Из пункта А в пункт В вышел пешеход со скоростью 5 км/ч. Одновременно с ним из А в В выехал велосипедист со скоростью 10км/ч. Велосипедист доехал до В, повернул назад и поехал с той же скоростью навстречу пешеходу. Через сколько часов после начала движения они встретятся, если расстояние между А и В 30км?
Б) Из пункта А в пункт В, расстояние между которыми 17 км, выехал велосипедист со скоростью 12 км/ч. Одновременно с ним из А в В вышел пешеход со скоростью 5 км/ч. Велосипедист доехал до В, повернул и поехал назад с той же скоростью. Через сколько часов после начала движения они встретятся?
Решение:
А)
T=S/U= 30/10=3 часа (велосипедист доехал до В)
S=UxT=5×3=15км (за 3 часа прошел пешеход)
Uсближения=U1+U2=10+5=15км/ч – скорость сближения
T=S/U=15/15=1 ч (преодолели 15 км вместе)
3ч+1ч=4 часа – встретились велосипедист и пешеход.
Б)
Велосипедист за 1 час проедет 12км, за 2 часа – 24км
24-17=7км
Пешеход за 2 часа пройдет 5х2=10км
10+7 =17, значит через 2 часа они встретятся.